Modelos de Markov: recomendações sobre boas práticas da Task Force ISPOR/SMDM

No nosso post de hoje, seguimos com o assunto modelagem, focando no modelo que é mais frequentemente visto na análise de custo-efetividade de doenças crônicas – o modelo de Markov. Conforme nossa postagem da semana passada, ele nem sempre é o modelo mais indicado, sendo sempre importante como primeiro passo conferir se não há um detalhe sobre a modelagem em questão que contraindique seu uso (veja na nossa postagem anterior tais situações).

Nos próximos parágrafos, revisitamos alguns pontos de importante artigo de Siebert e col., fruto de uma Task Force conjunta da ISPOR e SMDM, onde são dadas recomendações de melhores práticas acerca da utilização de modelos de Markov e destacadas importantes diferenças entre modelos de Markov com simulação de coorte daqueles que empregam micro-simulação.

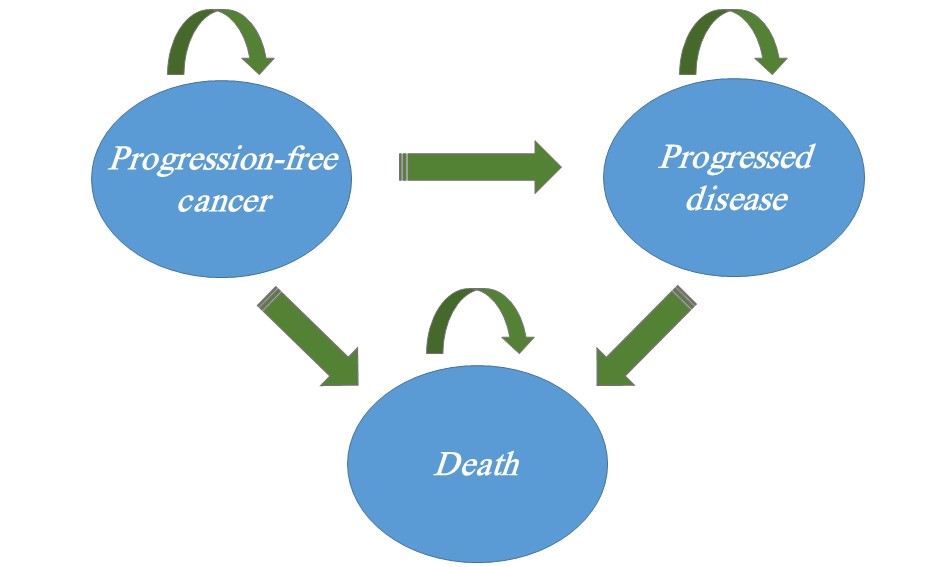
Os elementos de um modelo de Markov são estados de saúde (e definição de fração de início em cada estado), transições (e suas probabilidades), duração de ciclo, valores associados a cada estado (state rewards, que correspondem aos custos e desfechos em saúde – por exemplo, anos de vida – acumulados durante a permanência em determinado estado de saúde), testes lógicos realizados no início de cada ciclo para determinar transições e condição de término.

Os estados de saúde representam as possíveis situações que os pacientes se encontram (por exemplo: sem câncer, câncer estágio I, II e assim por diante), os quais deveriam ser exaustivos (ou seja, representar todas as possibilidades clínicas para um paciente) e mutuamente exclusivos (isto é, os pacientes só podem estar em um estado a cada momento do tempo).

Existem duas maneiras de construir um modelo de Markov: por simulação de coortes ou por micro-simulação. O primeiro é mais simples e mais conhecido pelo público leitor, porém, eles têm ausência de memória (memoryless), isto é, eventos prévios não afetam eventos futuros (exceto se criado um estado específico que represente esta característica). A micro-simulação é mais poderosa em termos de modelagem, mas sua construção é mais complexa, usualmente sendo necessário simular mais de meio milhão de indivíduos para que se consiga estabilidade nas estimativas. Quando é necessário rodar uma análise de sensibilidade probabilística, é necessário então cruzar estes milhares (ou milhões) de indivíduos simulados com milhares de conjuntos de parâmetros, o que pode necessitar de vários dias de rodagem de simulação mesmo em computadores modernos. Portanto, a micro-simulação deve ser utilizada somente quando realmente se mostrar necessária, isto é, quando criar diferentes estados para representar toda a heterogeneidade clínica torne o modelo de coortes difícil de gerenciar em decorrência da proliferação de estados.

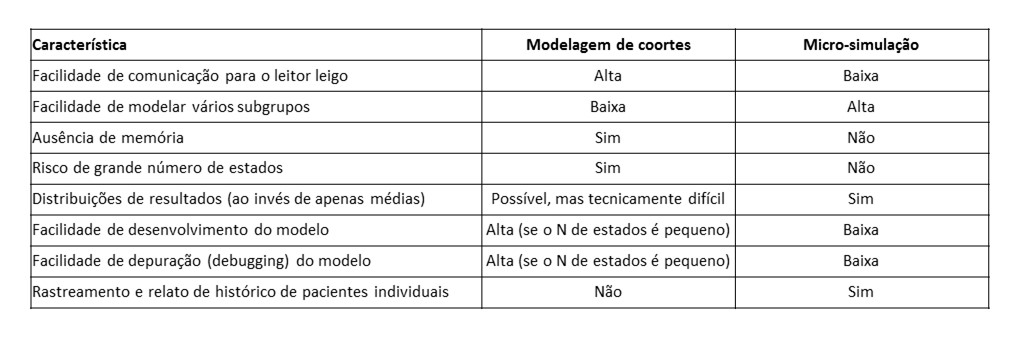
O quadro abaixo traça comparação entre a simulação de coortes e a micro-simulação.

A seguir, são listadas as recomendações de melhores práticas acerca da utilização de modelos de Markov:

1. A escolha de um modelo de Markov é adequada quando o problema puder ser representado em termos de estados de saúde, interações entre indivíduos não forem relevantes, e a população de interesse seja uma coorte fechada.
2. Caso o problema possa ser representado por um número gerenciável de estados de saúde que incorporem todas as características relevantes ao problema de decisão, a preferência se dá pela simulação de coorte, tendo em vista sua transparência, eficiência e facilidade de depuração (debugging) e de realização de análises de sensibilidade. Caso o número de estados necessários seja muito grande, deve-se preferir a micro-simulação.
3. A coorte que inicia o modelo deve ser claramente definida em termos de características clínicas e demográficas que afetem probabilidades de transição e state rewards (valores de efetividade e custos).
4. A especificação dos estados e das transições entre os mesmos deveria refletir o conhecimento teórico acerca da doença que está sendo modelada.
5. Caso existam eventos imediatos ou de curto prazo a serem considerados no modelo, eles podem ser representados antes do nodo de Markov, isto é, em uma árvore de decisão que precede o Markov.
6. Os benefícios, malefícios e custos das intervenções deveriam ser adequadamente capturados nos diferentes estados.
7. A duração do ciclo deveria ser curta o suficiente para representar a frequência de eventos clínicos, isto é, do ponto de vista clínico, não deveria ser possível sofrer mais do que um evento a cada ciclo. Especialmente em casos de curta expectativa de vida (câncer metastático, por exemplo), o tamanho do ciclo deveria ser curto (semanas ou meses).
8. As probabilidades de transição devem ser derivadas das fontes de dados mais representativas para o problema de decisão. As probabilidades de transição relacionadas à história natural da doença deveriam ser idealmente derivadas de estudos epidemiológicos conduzidos nacionalmente. Na ausência destes, dados de estudos internacionais precisam ser utilizados; porém, possíveis diferenças destes para a realidade brasileira devem ser avaliadas em análise de sensibilidade. Outra opção é recuperar os dados de braço controle de ensaio clínico, apesar de a população neste tipo de estudo ser muito mais selecionada que a população alvo do modelo. Quando existirem várias fontes de informação para probabilidades, as mesmas devem ser agregadas por meio de metanálise de braço único (single groups meta-analysis). Uma descrição detalhada da busca das estimativas de todos os parâmetros do modelo, fontes efetivamente utilizadas e o racional para a amplitude avaliada na análise de sensibilidade devem ser fornecidos na descrição metodológica do estudo, usualmente em um apêndice.
9. Geralmente, os dados necessários para estimativas de parâmetros não são derivados diretamente da literatura, isto é, os dados disponíveis não estão no mesmo formato que o necessário (por exemplo, estudos reportam probabilidade de morte por câncer em cinco anos, quando o modelo requer a probabilidade em um ano). Nestas situações, todos os métodos e pressupostos usados para derivar estimativas de parâmetros da literatura devem ser reportados.
10. Os dados sobre efeito das intervenções usualmente são provenientes de ensaios clínicos randomizados ou de metanálises dos mesmos, quando houver mais de um estudo. Para intervenções onde se espera menor aderência dos pacientes do que o observado em ensaios clínicos, um ajuste dos dados para levar em consideração esta possível menor aderência no cenário clínico habitual pode ser feito. Também é possível que – especialmente na ausência de ensaios clínicos – sejam utilizados dados de estudos observacionais para estimativa de efetividade; porém, ajustes para confundimento (por técnicas de regressão ou escores de propensão – propensity scores) necessitam ser feitos. Quando o horizonte temporal do modelo é muito maior do que o seguimento do ensaio clínico, e o principal parâmetro utilizado é a redução de mortalidade geral, a estimativa do ensaio clínico pode requerer ajuste. Isto porque a mortalidade por outras causas que não a doença modelada aumenta com a idade, e, consequentemente, o benefício da intervenção provavelmente diminui ao longo do tempo neste parâmetro.
11. Deve ser utilizada correção de meio de ciclo, uma vez que a sua não utilização assume que as transições se dão todas ao final do ciclo, o que não é a verdade na maioria das situações clínicas.
12. Em modelos onde se utiliza micro-simulação, o número de indivíduos simulados deve ser grande o suficiente para produzir estimativas estáveis.
13. Para a apresentação do modelo, é interessante que seja utilizado um diagrama de bolhas (bubble diagram) e/ou uma árvore de Markov.
14. Para a apresentação do modelo, é interessante que desfechos intermediários também sejam apresentados. Isto é especialmente factível em modelos de microsimulação, onde se pode apresentar, além dos anos de vida ganhos, a proporção de pacientes que sofreu um infarto do miocárdio ou um acidente vascular cerebral, em um modelo de prevenção cardiovascular, por exemplo.